1 – SMRT presentation
Several active microwave radiative transfer models were developed to simulate the total backscattering coefficient from a multilayered snowpack (DMRT-QMS, MEMLS, etc.) in various angular and polarimetric configurations. They are particularly well adapted for high-frequency radar (Ku band and higher frequencies) due to multiple scattering implementations. They are well known and widely shared in the snow microwave community. The Snow Microwave Radiative Transfer (SMRT) model recently developed in the framework of the ESA project “Microstructural origin of electromagnetic signatures in microwave remote sensing of snow” starting in 2015, also computes the total backscatter model of snowpack in the microwave domain in addition to the thermal emission. More precisely, the targeted validity is in the range 1-200 GHz, but not all the components are fully valid yet for the upper frequency range. For most snowpack, the validity is reasonable at Ku and Ka bands, which is relevant for this study. Compared to similar existing models such as MEMLS or DMRT-QMS, SMRT was developed to unify and inter-compare different descriptions of the snow microstructure found in different microwave models. For that, SMRT offer the capability of switching between different electromagnetic theories, representations of snow microstructure, and other modules involved in various calculation steps. SMRT is driven with snowpack properties (thickness, density, temperature and snow grain size, liquid water content for each layer) and the properties of the underlying surface (type of materials, roughness, wetness, salinity, etc.). With the active configuration, SMRT simulates total backscattering coefficients at different polarizations and incidence angles. SMRT is written in Python and clearly structured and modular, allowing easy intercomparisons between different modelling approaches and extension.
https://github.com/smrt-model/smrt
2 – Altimetry simulations over snow surface: state of the art
The altimetry waveform is the backscattered power measured at the satellite as a function of the time from the emission of a pulse of microwaves:
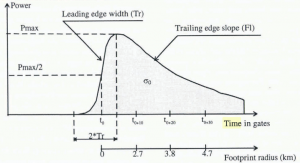
Waveform parameters description, by Legresy and Remy (1997).
Formulations for the surface backscatter (oceanic surface) has been proposed by Brown (1977), who showed that the received signal is the convolution of 1) the emitted pulse signal 2) the return delay due to surface height variations (roughness) around the mean surface and 3) a time function (PFS) accounting for the progressive return within the footprint, from the center (at nadir) to the side of the footprint.. The PFS proposed by Brown formally writes:
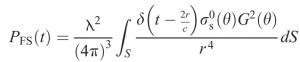 [1]
[1]
where G is the antenna known and σs (also called sigma naught) the surface backscatter. r is the distance from the surface to the satellite.
For penetrable media such as snow and ice, the signal has an additional component, called “volume” in the altimetry community, because it comes after (below) the surface, but based on the nomenclature used by 1st order radar modelers, this component indeed includes volume scattering and backscatter from the snowpack internal interfaces. This component is convoluted with the other components (see 1, 2, 3).
This theory is in principle adequate when the dominant reflection of energy comes from the snow-ice interface and to build the radar echo received by the satellite by neglecting the snow-air interface and volume scattering (Kurtz et al., 2014; Davis et al., 2017). Nevertheless, this assumption is not realistic when the snow cover contains wet or saline layers, which is the case for snow cover over sea ice, or for deep snow as on the ice sheets.
A few studies created a waveform simulator for ice sheet backscatter by converting the total backscattering simulated for a single layer snowpack (Ridley and Partington, 1988) or for a multi-layer snowpack (Legrésy and Rémy, 1997) to the backscattered power as a function of time using loss factor to account for the extinction of the wave in the snowpack, first order theory and time travel based on geometrical consideration. Nevertheless, they used simplified analytical equations to estimate volume scattering, and not a detailed radiative transfer model (Rémy, 2012). Tonboe et al. (2006a) used the MEMLS multilayer radiative transfer model to simulate scattering and extinction for each layer ( under Improve Born Approximative, IBA, Mätzler, 1998), and an empirical reflection formulation (close to geometrical optics) for the surface (Fetterer et al., 1992), but they neglected the internal interfaces.
From these pioneering studies and implementation, Lacroix et al. (2008) built a model for the ice-sheets, using the Improve Born Approximative for the volume, and the Integral Equation Model (IEM, Fung et al. 1992) for the surface and interfaces. Both approximations have proved their performance, and their validity range is relatively well established. Lacroix’ model is a first order model, that is, it only computes single scattering. For the propagation of the wave, it uses the result of Adams and Brown (1998) to adapt the Brown model to a multi-layered snowpack. The sub-surface model is the convolution of the PFS and the vertical distribution of the scattering properties of the medium. The surface contribution depends on the snow density heterogeneity and roughness features, and the volume contribution depends of scattering by snow grains, i.e of snow grain size. Hence, the ‘flat volume’ impulse response of a multi-layered snowpack is written as follows (Lacroix et al., 2008):
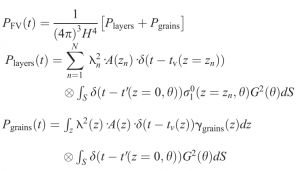 [2],
[2],
with A(z) the extinction at the depth z, N is the number of internal layers, λn is the radar wavelength at the depth of the layer n, zn. dz is computed considering the dielectric properties of the medium.
3 – SMRT adaptations to altimetry
The review showed that several altimetry models have been developed, with all having some identifiable limitations. The most stringent issue is that they are not widely available, so not widely used and as a consequence are not well validated. They also are somewhat incomplete, because the authors have made a series of fixed/hard coded choices (theories, assumptions, …) for the many different components, which may be relevant for their specific application but makes such models difficult to apply in other conditions. It results that their usability is very low.
SMRT was built from 2015 with the aim to make available the existing diversity of modelling work (of historical interest only for some of them) in a unique code base, accessible to a wide public, with the hope: 1) to promote validation and contribution by the community, and 2) to facilitate future implementations of models by building on existing, solid, components instead of re-building all the components every time. The adaptation of SMRT to radar altimetry follows this same strategy and really benefits for it. The only necessary addition is the time-dependent radiative transfer solver needed for the altimetry, almost all the other components for media (snow, ice, sea-ice), volume and interface scattering theories, etc are already available in SMRT, well tested.
The new “nadir_altimetry” solver in SMRT follows Lacroix et al. (2008) and Adams and Brown (1998). Once the medium is defined by the user, and scattering and propagation properties for each layer and interfaces are calculated using the existing SMRT modules (see Picard et al. 2018), the “nadir_altimetry” solver aims at solving the propagation in the air and in the medium of the wave over the footprint area. Lacroix et al. 2008 and Adams and Brown 1998 demonstrate that this can be achieved in two independent steps:
- 1) the propagation in the medium, from the surface to the internal layers,
- 2) the propagation in the air from the altimeter to the surface (and back).
The second step corresponds to the calculation of the PFS, and is a solved problem since Brown 1977. It is also already implemented in AltiDop with many more details (ie. less restrictive assumptions) than in Brown 1977, enabling to take into account the subtleties of the sensors and terrain topography. SMRT implements the Brown model as a side product of this project, enabling to produce waveforms for a flat surface.